
There are three numbering systems that every network engineer needs to know decimal, binary, and hexadecimal. We all know how the decimal system work, so let’s begin with the introduction to the binary system.
A basic understanding of the binary system and how to convert to a decimal system is an essential tool for anyone working as a network engineer. Therefore, you will find a few questions about binary numbers in your next CCNA or CompTIA exam.
Basics of Binary Numbers
Firstly, before I start talking about a good old computer networking conversation. Let’s start by introducing some of the basics of binary calculations. As a kids, we all learn how to use the decimal system. My daugher is 3 years old and already learning to count to 10. This is easy because most of us have 10 fingers so we don’t have to count off the top of our head.
Computer, networking devices, and machines used the binary system because of its simplicity of using only 1s and 0s. For a machine using electrical signals, it’s easier to communicate using only two states. 1 for On and 0 for Off.

All calculations in a computer are based on millions of transistors that are either in an ON or OFF position. In binary, the numbers 0s and 1s do not simply mean that the computer is on or off. To clarify, these ON and OFF signals can be interpreted by devices to achieve a broad range of results.
In order to understand how a computer network works you need to learn how to convert a number from binary to digital or hexadecimal. This is a basic knowledge you need to obtain while learning how to interact with IP Addresses and subnetting in a network.
How to convert decimal numbers to binary?
Firstly, let’s do a recap. To clarify, binary is a numerical notation system that uses 0s and 1s. Most often, numbers are represented by the Decimal system, which is base 10.
- Decimal: (deci)mal → (deci) meaning 10. → 110
- Binary: (bi)nary → (bi) meaning 2. → 12
In the decimal system, there are ten unique numbers from 0 to 9. In the binary system, there are only two unique numbers: 0 and 1. Each number is commonly known as a bit.
If you are preparing for a CCNA or Network+ exam you will need to learn how to convert an IP Address into a binary number. Let’s look at the following example. Use the table to convert from a decimal to a binary number or vice versa. Here is an example.
Basic Decimal to Binary Conversion Table
| Exponent | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| Decimal | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| Binary | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
Ex. If we want to convert the binary number 10100110 into a decimal form.
Plug the numbers from right to left and add the decimal number shown in the same column. Each column represents the number two raised to an exponent. Moreover, that exponent’s value increasing by one as you move through each of the eight positions.
To clarify, read the table from right to left. In addition, add each column’s value from the decimal row to the value on the previous column: (128+32+4+2) = 166. As you can see, we do not count the bits with a 0 because they’re “turned off.”
In the real world, you can use a calculator to do this conversion.
How to Convert an IPv4 Address into Binary
Let’s start by understanding what is IPv4 address. IPv4 is a 32-bit number that uniquely identifies a network interface on a machine. That is to say, an IPv4 address is typically written in decimal digits, formatted as four 8-bit long octets or segments separated by periods. In addition, every octet and must be a decimal value between 0 and 255.
For example, I will be using the Decimal to Binary Converting Table to convert the following IPv4 addresses into their binary form.
| Ex.1 | 192.168.0.12 | 11000000.10101000.00000000.00001100 |
| Ex.2 | 172.16.0.5 | 10101100.00010000.00000000.00000101 |
| Ex.3 | 10.0.1.11 | 00001010.00000000.00000001.00001011 |
Introduction to IPv6 Address

Now that you understand the binary system let’s move into the hexadecimal system. This numerical system has become a very important element of the computer world. As a result of the rapid increase of network-connected devices. Therefore, due to the necessity to maintain unique identifiers force the industry to include hexadecimal numbers. This new address system is called IPv6.
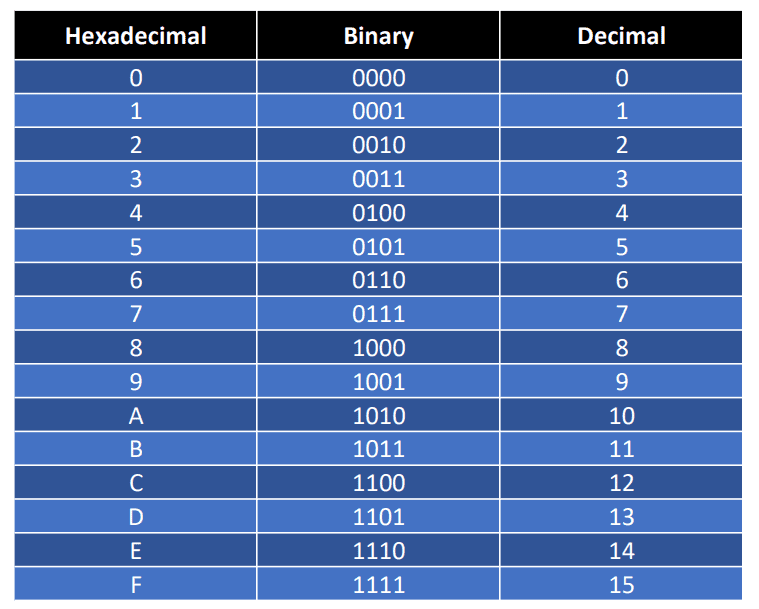
First, let’s begin by introducing the hexadecimal number system. This numerical system is also known as hex or as base-16 number system. It consists of 16 alphanumeric characters that include a range of numbers from 0 to 9 and a set of alphabet letters from A to F.
An IPv6 address format consists of eight groups or segments of hexadecimal values separated by colons. In addition, the first 64 bits of the IPv6 address are used for routing purposes. It consists of the routing prefix and subnet ID.
The last 64 bits identify the address of the interface or interface ID. In other words, it derived from the physical or MAC address using IEEE’s Extended Unique Identifier (EUI-64) format.
Convert an IPv6 Address into Decimal or Binary
Similar to IPv4 addresses, you can convert an IPv6 address into the binary system. The following chart will help you simplify the process.
For example, given below is a 128 bit IPv6 address represented in binary format and divided into eight 16-bits blocks:
0010000000000001 0000000000000000 0011001000111000 1101111111100001 0000000001100011 0000000000000000 0000000000000000 1111111011111011
Each block is then converted into Hexadecimal and separated by ‘:’ symbol:
2001:0000:3238:DFE1:0063:0000:0000:FEFB
Even after converting into Hexadecimal format, the IPv6 address remains long. IPv6 provides some rules to shorten the address.
How to Simplify or Compress an IPv6 Address
In addition to an increase in the supply of IP addresses. IPv6 also addressed some of the IPv4’s weaknesses of an older IP address system. However, this longer type of IP address. Therefore, increasing the difficulty for the network engineer to remember the addresses.
Consequently, a simplifying trick called IPv6 address compression is applied to help network engineers to remember these types of IP addresses. Above all, making it easier to read by the human eye.
IPv6 Address Compression Rules
| Rules | Sample IPv6 Address |
|---|---|
| Drop all leading ZEROS in each group | FROM 2001:0000:3238:DFE1:0063:0000:0000:FEFB TO 2001:0:3238:DFE1:63:0000:0000:FEFB |
| If there are FOUR ZEROS in a group replace them with one ZERO | FROM 2001:0:3238:DFE1:63:0000:0000:FEFB TO 2001:0:3238:DFE1:63:0:0:FEFB |
| *If there are TWO groups of ZEROS next to each other replace them with two colons (::) *Only 1 per Address* | FROM 2001:0:3238:DFE1:63:0000:0000:FEFB TO 2001:0:3238:DFE1:63::FEFB |
The Bottom Line
In conclusion, the conversion between binary, decimal, and hexadecimal numbers are the backbone of the computer network. Therefore, this is the main reason IT professional certification includes these types of questions in their certification exams.






